
https://www.toptal.com/developers/sorting-algorithms
Sorting Algorithms
주어진 데이터들을 특정한 기준 혹은 순서(번호나 알파벳 순 같은 어휘)로 정렬하는 것은
컴퓨터 뿐만 아니라 도서관의 도서 분류나 상품 진열과 같이 실생활에서도 아주 중요합니다.
특히, (정렬 가능한 형식일 때) 잘 정렬된 데이터들은 *이진탐색으로 빠르게 데이터에 접근할 수 있습니다.
(* 이진탐색 : 정렬된 리스트에 중간을 골라, UP or DOWN? 물어보는 방식으로 반의 반의 반... 으로 탐색하는 것)
효율적인 탐색을 위해 다양한 정렬 알고리즘들이 존재하지만, 해당 포스트에서는
[Selection, Insertion, Bubble, Merge, Heap, Quick, Count, Radix] 정도만 알아보겠습니다.
목차
- Selection 선택
- Insertion 삽입
- Bubble 버블
- Merge 병합/합병
- Heap 힙
- Quick 퀵
- Counting 카운팅/계수
- Radix 기수
- big-O 시간복잡도 표
Selection Sort (선택 정렬)
가장 작은 녀석 부터 찾아 맨 앞에 있는 친구와 자리를 바꿔가며 차례로 줄 세우기를 반복하는 방법입니다.
- 리스트 전체에서 가장 작은 값 찾기 → 맨 앞 원소와 교체 → 리스트 앞자리 채워가며 반복
void SelectionSort(int[] arr)
{
int n = arr.Length;
for (int i = 0; i < n - 1; i++) // 맨 마지막에는 한 놈만 남기 때문에 n - 1
{
int minIndex = i;
for (int j = i + 1; j < n; j++) // i 보다 뒤에 있는 녀석들을 탐색
{
if (arr[j] < arr[minIndex]) // 보다 작은지 확인
{
minIndex = j;
}
}
// 자리 교체 (i + 1 회전)
int temp = arr[i];
arr[i] = arr[minIndex];
arr[minIndex] = temp;
}
}
Insertion Sort (삽입 정렬)
지금까지 정렬된 앞 부분에 뒤의 친구를 적절한 위치에 끼워 넣는 방법입니다.
(카드 게임할 때 손에 든 카드를 정리하는 느낌)
거의 정렬된 배열이라면 거의 O(n)이지만, 완전히 섞였다면 O(n²) 입니다.
- 앞에서부터 하나씩 꺼내어 → 정렬된 부분에 끼워넣기
void InsertionSort(int[] arr)
{
int n = arr.Length;
for (int i = 1; i < n; i++) // i의 초기값을 1로
{
int j = i - 1; // 이중 반복문으로 j는 i-1 인덱스 번호부터 확인
int key = arr[i];
// 정렬된 부분에서 key보다 큰 값들을 오른쪽으로 한 칸 이동
while (j >= 0 && arr[j] > key)
{
arr[j + 1] = arr[j];
j--;
}
arr[j + 1] = key;
}
}
Bubble Sort (버블 정렬)
바로 옆에 있는 두 값을 비교해서 작은 숫자를 앞으로 큰 숫자를 뒤로 이동하며 정렬하는 방법입니다.
Selection은 n회전이 증가할 때마다 리스트의 앞부분이 작은 값 들 순서로 채워져 나갔지만,
Bubble은 리스트의 뒷부분 부터 가장 큰 값이 채워져 나가며 정렬됩니다.
( 버블이 수면 위로 올라가듯, 큰 숫자가 리스트의 뒤로 '둥둥' 떠올라가는 느낌인거 같아요 )
- 딱 붙어있는 값 두개를 비교 → 큰 값을 하나씩 뒤로 보냄
void BubbleSort(int[] arr)
{
int n = arr.Length;
for (int i = 0; i < n - 1; i++)
{
for (int j = 0; j < n - i - 1; j++)
{
if (arr[j] > arr[j + 1])
{
// 큰놈을 뒤로 교체
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
}
Merge Sort (합병 정렬)
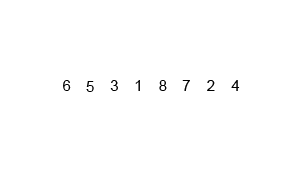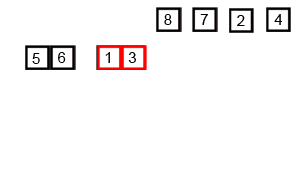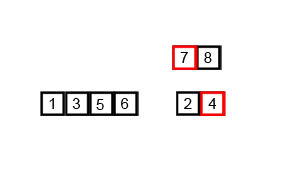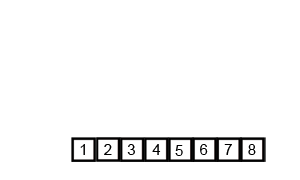
https://en.wikipedia.org/wiki/Merge_sort#/media/File:Merge-sort-example-300px.gif
Merge sort - Wikipedia
From Wikipedia, the free encyclopedia Divide and conquer sorting algorithm In computer science, merge sort (also commonly spelled as mergesort and as merge-sort[2]) is an efficient, general-purpose, and comparison-based sorting algorithm. Most implementati
en.wikipedia.org
Divide and Conquer 분할 정복 알고리즘으로, 재귀적으로 본인을 호출하며 (재귀함수) 연산할 단위를 줄여나가는 방법입니다.
Divide를 반복해 최소 단위로 만든 다음, Divide하고 난 다음에서야 정렬이 시작됩니다.
Conquer & Combie하고 다시 Conquer & Combie... 해 정렬된 리스트를 만듭니다.
추가적인 리스트 저장 메모리가 필요하게 되며, 공간복잡도는 O(n), 시간복잡도는 평균과 최악 둘 다 O(n log n)입니다.
항상 늘 O(n log n)가 나오니 대량의 데이터들을 정렬할 땐, Insertion이나 Bubble보다 안정적이라 볼 수 있습니다.
void MergeSort(int[] arr, int left, int right)
{
if (left < right)
{
int mid = (left + right) / 2; // 중간을 잘라 반토막 Divide
MergeSort(arr, left, mid); // 좌측 리스트 정렬 Conquer (재귀)
MergeSort(arr, mid + 1, right); // 우측 리스트 정렬 Conquer (재귀)
Merge(arr, left, mid, right); // 정렬된 리스트를 mid 기준으로 두개씩 합쳐나가기 Combine
}
}
void Merge(int[] arr, int left, int mid, int right)
{
int[] temp = new int[right - left + 1];
int i = left, j = mid + 1, k = 0;
// i 왼쪽 거 읽음
// j 오른쪽 거 읽음
// k 는 temp 포인팅 (zero부터 시작)
while (i <= mid && j <= right) // 왼/오 비교 후, 작은 놈을 temp에 저장
{
if (arr[i] <= arr[j])
temp[k++] = arr[i++];
else
temp[k++] = arr[j++];
}
// 아직 안끝났다면 그대로 temp에 저장 (이미 정렬됐으니 비교 끝)
while (i <= mid) temp[k++] = arr[i++];
while (j <= right) temp[k++] = arr[j++];
for (i = left, k = 0; i <= right; i++, k++)
arr[i] = temp[k];
}
Quick Sort (퀵 정렬)
기준값(pivot)을 기준으로 작은 값과 큰 값을 양쪽으로 나눈 다음, 이 과정을 반복하여 정렬하는 분할 정복 알고리즘입니다.
작동 방식 순서를 대략적으로 그리면,
- 기준값(Pivot)을 하나 선택합니다.
- 그 기준보다 작은 값은 왼쪽, 큰 값은 오른쪽으로 보냅니다. (이걸 Partition이라고 하나봐요)
- 이제 왼쪽과 오른쪽 각 구간에 대해 재귀적으로 퀵정렬을 합니다.
- 더 쪼갤 수 없을 때까지 반복합니다.
예시를 들자면,
[7, 3, 8, 4, 2, 6, 5]
- 피벗을 5로 잡습니다.
- 5보다 작은 놈들 : [3, 4, 2] → 왼쪽
5보다 큰 놈들 : [7, 8, 6] → 오른쪽 - 이렇게 나눈 다음에 양쪽도 똑같이 정렬합니다.
- 마지막에 합치면 정렬 완료...입니다.
Merge 처럼 분할 정복 (Divide and Conquer) 방식입니다. (but, Merge보다 빠르다네요)
void QuickSort(int[] arr, int left, int right)
{
// 정렬할 구간이 존재할 때만 수행
if (left < right)
{
// 분할 기준(pivot)의 위치를 찾고
int pivotIndex = Partition(arr, left, right);
// 왼쪽 부분을 재귀적으로 퀵 정렬
QuickSort(arr, left, pivotIndex - 1);
// 오른쪽 부분을 재귀적으로 퀵 정렬
QuickSort(arr, pivotIndex + 1, right);
}
}
int Partition(int[] arr, int left, int right)
{
int pivot = arr[right]; // 기준이 되는 피벗 값을 오른쪽 끝 값으로 선택
int i = left - 1; // 피벗보다 작은 값들이 모이는 구역의 마지막 인덱스
// left부터 right - 1까지 탐색하면서 피벗보다 작은 값들을 앞으로 보냄
for (int j = left; j < right; j++)
{
if (arr[j] < pivot)
{
i++; // 작은 값 구역 확장
// 현재 arr[j]를 arr[i]와 교환
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
// 최종적으로 피벗을 작은 값 구역의 다음 위치로 이동
int temp2 = arr[i + 1];
arr[i + 1] = arr[right];
arr[right] = temp2;
// 피벗의 최종 위치를 반환
return i + 1;
}
Heap Sort (힙 정렬)
완전이진트리 기반의 힙(Heap) 구조를 이용해, 가장 큰 값(or 가장 작은 값)을 하나씩 꺼내면서 정렬하는 방법입니다.
- Max Heap : 부모 노드가 자식 노드보다 항상 크거나 같습니다. (Parent >= Child)
- Min Heap : 부모 노드가 자식 노드보다 항상 작거나 같습니다. (Parent <= Child)
위에 따라, 최대 (Max) 힙은 내림차순 정렬, 최소 (Min) 힙은 오름차순 정렬이 됩니다.
작동 순서를 대략 그려보자면,
- 배열을 힙 구조(Max Heap)로 만듭니다. (즉, 배열의 맨 앞(arr[0])에 가장 큰 값이 오도록)
- 가장 큰 값을 꺼내어, 배열의 마지막으로 보냅니다. (맨 앞 값(arr[0])과 맨 뒤 값(arr[n-1])을 교환)
- 힙의 크기를 하나 줄이고(즉, 정렬 완료된 마지막 값은 제외), 다시 힙 구조를 유지합니다.
- 이 과정을 배열의 크기만큼 반복합니다.
void HeapSort(int[] arr)
{
int n = arr.Length;
// 배열을 최대 힙 구조로 바꿈 (힙 정렬의 준비 단계)
for (int i = n / 2 - 1; i >= 0; i--) // 중간부터 루트까지 역순으로 Heapify 호출
Heapify(arr, n, i);
// 힙에서 하나씩 꺼내어 정렬된 위치로 보냄
for (int i = n - 1; i >= 0; i--)
{
// 루트(최대값)를 끝으로 이동
int temp = arr[0];
arr[0] = arr[i];
arr[i] = temp;
// 남은 트리에 대해 다시 최대 힙을 유지
Heapify(arr, i, 0);
}
}
void Heapify(int[] arr, int n, int i)
{
int largest = i; // 현재 노드를 가장 큰 값으로 초기화
int left = 2 * i + 1; // 왼쪽 자식 인덱스
int right = 2 * i + 2; // 오른쪽 자식 인덱스
// 왼쪽 자식이 현재 노드보다 크면 largest 갱신
if (left < n && arr[left] > arr[largest])
largest = left;
// 오른쪽 자식이 현재 largest보다 크면 largest 갱신
if (right < n && arr[right] > arr[largest])
largest = right;
// 만약 자식 중 하나가 현재 노드보다 크다면, 교환하고 재귀 호출
if (largest != i)
{
int swap = arr[i];
arr[i] = arr[largest];
arr[largest] = swap;
// 바뀐 자식 기준으로 다시 Heapify 호출 (하향식으로 정리)
Heapify(arr, n, largest);
}
}
Counting Sort (카운팅 정렬)
숫자 하나하나를 비교하지 않고, '이 숫자가 몇 번 나왔는지'를 세는 방식으로 정렬합니다.
예시로 다음과 같은 배열이 있다고 해봅시다.
- 가장 큰 숫자(8)까지 카운트를 저장할 배열을 만듭니다.
→ [0, 0, 0, 0, 0, 0, 0, 0, 0] (0~8까지 9칸) - 각 숫자가 등장한 횟수를 써 놓습니다.
→ [0, 1, 2, 2, 1, 0, 0, 0, 1] - 위 카운트를 기반으로, 정렬된 결과를 채워 넣습니다.
→ [1, 2, 2, 3, 3, 4, 8]
비교없이 정렬하는 알고리즘이며, 값의 범위가 작고, 중복된 크기의 숫자가 많으며, 정수일 때 사용하게 됩니다.
제한사항으로는 범위가 너무 큰 정수나 음수나 실수는 처리하기 힘들다는 점이 있습니다.
또, Counting Sort는 비교 정렬이 아닙니다. (a>b 이런 비교 없이 정렬이 가능한 정렬이에용)
void CountingSort(int[] arr)
{
int max = arr.Max(); // 배열 내 가장 큰 값을 구함 (카운팅 배열의 크기를 결정하기 위해)
int[] count = new int[max + 1]; // 0부터 max까지의 값을 카운팅할 배열 생성
// 각 숫자의 등장 횟수를 count 배열에 저장
foreach (int num in arr)
count[num]++;
int index = 0; // 정렬된 값을 원래 배열에 다시 넣기 위한 인덱스
// count 배열을 순회하며, 각 숫자를 등장 횟수만큼 arr에 채움
for (int i = 0; i < count.Length; i++)
{
// count[i]가 0이 될 때까지 i를 arr에 채움
while (count[i]-- > 0)
{
arr[index++] = i; // 해당 숫자를 arr에 넣고 인덱스를 증가
}
}
}
Radix Sort (기수 정렬)
숫자의 자릿수 별로 정렬을 반복해서 정렬하는 알고리즘입니다.
1의 자리 → 10의 자리 → 100의 자리 (가장 작은 자리부터 큰 자리까지 차례대로)
위와 같은 방식으로 각 자릿수를 기준으로 정렬을 여러 번 반복해 전체 숫자를 정렬하는 방식입니다.
얘도 Counting Sort처럼 정수들이 많고, 숫자 자릿수도 적을때 유용한 알고리즘입니다.
Radix Sort도 비교 기반 정렬이 아닌, 자릿수를 나눠 처리하는 독특한 정렬입니다.
그래서 특히 많은 데이터를 정수로 정렬할 때 Quick Sort, Merge Sort 같은 O(n log n)보다 더 빠를 수도 있습니다.
void RadixSort(int[] arr)
{
int max = arr.Max(); // 가장 큰 숫자를 찾아서 몇 자리수까지 있는지 확인
// 자리수(exp: 1의 자리, 10의 자리, 100의 자리...)를 기준으로 반복
for (int exp = 1; max / exp > 0; exp *= 10)
CountSortByDigit(arr, exp); // 각 자리수 기준으로 Count Sort 수행
}
void CountSortByDigit(int[] arr, int exp)
{
int n = arr.Length;
int[] output = new int[n]; // 정렬 결과를 담을 배열
int[] count = new int[10]; // 0~9까지 각 자리 숫자 빈도 수를 저장
// 현재 자리수(exp)에 해당하는 숫자 자리를 기준으로 카운트
for (int i = 0; i < n; i++)
count[(arr[i] / exp) % 10]++;
// 누적 합을 구해서 실제 위치 계산 (안정 정렬을 위해)
for (int i = 1; i < 10; i++)
count[i] += count[i - 1];
// 배열을 뒤에서부터 탐색하면서 정렬된 위치에 넣음 (안정성)
for (int i = n - 1; i >= 0; i--)
{
int digit = (arr[i] / exp) % 10; // 현재 자리수의 숫자 추출
output[count[digit] - 1] = arr[i]; // 해당 숫자의 위치에 값 저장
count[digit]--; // 같은 숫자 다음 위치를 가리키도록 감소
}
// 정렬된 결과를 원본 배열로 복사
for (int i = 0; i < n; i++)
arr[i] = output[i];
}
big-O 시간복잡도
| Algorithm | Space Complexity | Average Time Complexity | Worst Time Complexity |
| Selection sort | O(1) | O(n²) | O(n²) |
| Insertion sort | O(1) | O(n²) | O(n²) |
| Bubble sort | O(1) | O(n²) | O(n²) |
| Merge sort | O(n) | O(n log n) | O(n log n) |
| Heap sort | O(1) | O(n log n) | O(n log n) |
| Quick sort | O(log n) | O(n log n) | O(n²) |
| Counting sort | O(k) | O(n + k) | O(n + k) |
| Radix sort | O(n + k) | O(nk) | O(nk) |
Bogo Sort (보고 정렬)
랜덤으로 데이터를 배열하고 잘 정렬됐는지 확인하는 짓을 반복합니다.
평균 복잡도는 O(n × n!)이지만, 잭팟 터지면 O(n)이라 시도해 볼만 합니다.

여기까지 정렬 알고리즘을 정리해봤습니다.
(퀵소트부턴 귀찮아서 한 번 때려쳤다가... 😂 다시 이어서 썼어용)
그냥 보면 어렵지 않은데, 막상 백지에 직접 짜보려고하면 은근 어려운 알고리즘입니다.
그러니 좌절하지 마시고 조금만 참고 이겨내어 저희 걸로 만들어 갑시다.
오늘 하루도 화이팅! (ノ´∩。• ᵕ •。∩)ノ
'- Algorithms > (Bul)ALGO(Ja)rithms' 카테고리의 다른 글
| [Algorithm] Brute Force 브루트 포스 (0) | 2025.06.16 |
|---|---|
| [Algorithm] Euclidean algorithm GCD 유클리드 호제법 최대공약수 (0) | 2025.06.15 |
| [Algorithm] Caesar Cipher 시저 카이사르 암호 (0) | 2025.05.06 |
