[Graphics] HLSL Vector 벡터 메서드 정리

벡터(Vector)

HLSL에서 벡터(Vector)는 조명 계산, 좌표 변환, 텍스처 좌표 처리 등에서 자주 사용되는 자료형입니다.

기본적인 것들 먼저 살펴보겠습니다.

 

---

벡터 관련 주요 메서드

	메서드	내용
	dot(a, b)	내적 (두 벡터의 유사도)
	cross(a, b)	외적 (두 벡터가 만드는 수직 벡터)
	normalize(v)	정규화 (길이 1짜리 단위(unit) 벡터로, x/length(x) )
	length(v)	벡터의 길이 (선형대수학의 norm과 같음, |v| )
	reflect(I, N)	반사 벡터 계산 (입사 I, 노멀 N)

 

dot() 내적

내적, 두 벡터의 크기를 서로 곱한 후 두 벡터 간의 각도 코사인을 곱한 값입니다.

a ⋅ b = |a| |b| cosθ

 

내적은 결과로 float 타입의 스칼라(Scalar)값을 뱉어냅니다.

위 식에서 양변을 |a| |b| 로 나눈다면,

 

만약, |a| = |b| = 1 의 단위벡터라면,

a ⋅ b = cosθ

 

즉, a와 b 의 norm이 1일때, 내적 결과는 두 벡터 사이의 각도 정보를 그대로 표현하게 됩니다.

• 같은 방향일 때 → cos(0) = 1

float3 A = normalize(float3(1, 0, 0)); // x축 방향
float3 B = normalize(float3(2, 0, 0)); // 같은 x축 방향
float result = dot(A, B); // 결과 : 1

• 반대 방향일 때 → cos(π) = -1

float3 A = normalize(float3(1, 0, 0)); // x축
float3 B = normalize(float3(-1, 0, 0)); // 반대 x축
float result = dot(A, B); // 결과 : -1

• 수직 방향일 때 (내적은 수직할 때 0 이에요) → cos(π/2) = 0

float3 A = normalize(float3(1, 0, 0));   // x축
float3 B = normalize(float3(0, 1, 0));   // y축
float result = dot(A, B); // 결과 : 0

 

셰이더에서는 이 점을 활용해 광원의 각도에 따라 밝기 조절을 한다거나, 라이팅 계산에 이용할 수도 있습니다.

float3 normal = normalize(IN.normal);
float3 lightDir = normalize(_WorldSpaceLightPos0.xyz);
float intensity = dot(normal, lightDir); // 조명 밝기 결정

 

위 intensity 값은 보통 0~1 범위로 조정되며, 조명 밝기 또는 디퓨즈 컬러 강도에도 사용됩니다.

 

cross() 외적

a, b 두 벡터가 이루는 평면(평행사변형)에 수직인 벡터(Vector)를 반환합니다.

 

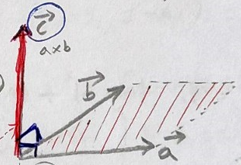
위 그림은 a × b = c 해서 a와 b 벡터에 수직하는 벡터를 반환한 그림입니다.

그렇다면 외적 결과에 크기는 어떤의미를 가지게 될까요?

|a × b| = |a| |b| sinθ

 

내적은 수직할 때 0이지만, 외적은 두 벡터가 수직(sin90º = 1)일 때 가장 큰 크기를 가지며,

평행하다면 0이 나옵니다.

 

외적(Cross Product)의 정의는 위와 같으므로, 아래 코드 처럼 작성이 가능합니다.
(영문 위키피디아에 설명 잘 돼있어요 https://en.wikipedia.org/wiki/Cross_product)

 

float3 tangent = float3(1, 0, 0);
float3 normal = float3(0, 1, 0);

float3 bitangent = cross(normal, tangent); // 결과 : (0, 0, -1)

 

bitangent 벡터는 normal과 tangent에 수직인 벡터입니다. (Tangent Space (법선 매핑) 계산)

 

Normalize() 정규화

(저만 선형대수학의 norm과 헷갈렸나요...ㅠㅠ)

벡터의 방향은 유지하며 길이(length)를 1로 만든 단위 벡터(Unit Vector)를 반환합니다.

normalize(v) = v / |v|​

float3 dir = float3(2, 4, 4);
float3 unitDir = normalize(dir); // 방향은 같고 길이는 1인 단위 벡터

 

벡터의 길이(크기)에 관계없이 안정적인 연산을 위해 단위 벡터로 정규화하는 작업이 중요합니다.

 

Length() 길이

네, 수학에서 배우는 그 벡터의 놈 / 놂 / 노름 (Euclidean norm)과 같은 겁니다.

|v| = √(x² + y² + z²​)

 

코드로 간단히 증명하면,

float3 v = float3(3, 4, 12);
float len = sqrt(v.x * v.x + v.y * v.y + v.z * v.z); // = 13

 

간단하게 sqrt(x² + y² + z²) 로 생각하시면 됩니다.

(아래는 재밌는 생각나서 추가해봤어용, 내적은 자기 자신 내적 했을 때 제곱한 크기와 같거든요)

float3 v = float3(3, 4, 12);
float len1 = length(v); // 길이 계산
float len2 = sqrt(dot(v, v)); // 수학적으로 같은 의미

 

Reflect()

벡터 I가 법선 벡터 N에 대해 반사되는 벡터를 반환합니다.

말 그래도 거울이나 물 표면 등에 반사되는 겁니다.

reflect(I, N) = I - 2 * N * dot(I, N)

• I는 입사 벡터 (빛이나 시선 방향)
• N은 법선 벡터 (반사 표면의 방향)

단순하게, 반환값은 반사된 벡터 값입니다.

float3 viewDir = normalize(worldViewDir);
float3 normal = normalize(worldNormal);

float3 reflection = reflect(-viewDir, normal); // 거울에 반사된 방향

 

---

 

솔직히 엄청 어려운 개념들은 아니지만,

보기 좋은 그래픽을 만들기 위해서라면,

꽤 복잡해지고 어려워질 거 같습니다.

하지만 차근차근 구준히 하다보면 꼭! 멋진 그래픽을 만들 수 있을 거에요!

오늘도 좋은 하루 되시길 바랍니다! (*ᴗ͈ˬᴗ͈)ꕤ*.ﾟ

 

참고 : http://www.silverwolf.co.kr/shader/79529